Critical pair (logic)

In mathematical logic, a critical pair arises in term rewriting systems where rewrite rules overlap to yield two different terms.

For example, in the term rewriting system with rules

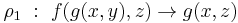
$\rho_1\�:\ f(g(x,y), z) \rightarrow g(x,z)$

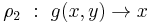$\rho_2\�:\ g(x,y) \rightarrow x$ ,

the only critical pair is then (g(x,z), f(x,z)).

When one side of the critical pair reduces to the other, we say that the critical pair is convergent. Where one side of the critical pair is identical to the other, we say that the critical pair is trivial.

Note that if the term rewriting system is not confluent, the critical pair may not converge, so critical pairs are potential sources where confluence will fail. In fact, we have the critical pair lemma, which states that a term rewriting system is weakly confluent if all critical pairs are convergent. Thus, to find out if a term rewriting system is weakly confluent, it suffices to test all critical pairs and see if they are convergent. This makes it possible to find out algorithmically if a term rewriting system is weakly confluent or not.

Weak confluence clearly implies convergent critical pairs: if any critical pair (a, b) arises, then a and b have common reduct and thus the critical pair is convergent.

External links

Weisstein, Eric W., "Critical Pair" from MathWorld.

References

Franz Baader and Tobias Nipkow, Term Rewriting and All That, Cambridge University Press, 1998 (book weblink)
Terese, Term Rewriting Systems, Cambridge Tracts in Theoretical Computer Science, 2003. (book weblink)